Filter Example¶
This example demonstrates the connection between MKS and signal processing for a 1D filter. It shows that the filter is in fact the same as the influence coefficients and, thus, applying the LocalizationRegressor is in essence just applying a filter.
[1]:
%load_ext autoreload
%autoreload 2
[45]:
import numpy as np
import matplotlib.pyplot as plt
import scipy.ndimage
from sklearn.pipeline import Pipeline
from pymks import (
PrimitiveTransformer,
LocalizationRegressor,
coeff_to_real
)
Construct a filter, \(F\), such that
Try to show that, if \(F\) is used to generate sample calibration data for the MKS, then the calculated influence coefficients are in fact just \(F\).
[7]:
def filter_(x):
return np.exp(-abs(x)) * np.cos(2 * np.pi * x)
[41]:
x = np.linspace(-10.0, 10.0, 1000)
y = filter_(x)
plt.plot(x, y, color='#1a9850');
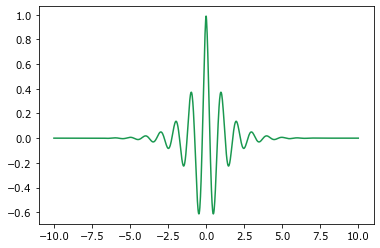
Next, generate the sample data using scipy.ndimage.convolve. This performs the convolution
for each sample.
[21]:
np.random.seed(201)
def convolve(x_sample):
return scipy.ndimage.convolve(
x_sample,
filter_(np.linspace(-10.0, 10.0, len(x_sample))),
mode="wrap"
)
x_data = np.random.random((50, 101))
y_data = np.array([convolve(x_sample) for x_sample in x_data])
[22]:
print(x_data.shape, y_data.shape)
(50, 101) (50, 101)
For this problem, a basis is unnecessary, as no discretization is required in order to reproduce the convolution with the MKS localization. Using the PrimitiveTransformer with n_state=2 is the equivalent of a non-discretized convolution in space.
[33]:
pipeline = Pipeline(steps=[
('discretize', PrimitiveTransformer(n_state=2)),
('regressor', LocalizationRegressor())
])
pipeline.fit(x_data, y_data)
y_predict = pipeline.predict(x_data)
fcoeff = pipeline.steps[1][1].coeff
print(y_predict[0, :4].compute())
print(y_data[0, :4])
print(fcoeff.shape)
[-0.41059557 0.20004566 0.61200171 0.5878077 ]
[-0.41059557 0.20004566 0.61200171 0.5878077 ]
(101, 2)
[44]:
x = np.linspace(-10.0, 10.0, 101)
coeff = coeff_to_real(fcoeff, (101,))
plt.plot(x, filter_(x), label=r'$F$', color='#1a9850')
plt.plot(x, -coeff.real[:, 0] + coeff.real[:, 1],
'k--', label=r'$\alpha$')
l = plt.legend()
plt.show()
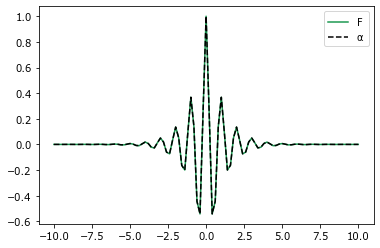
Some manipulation of the coefficients is required to reproduce the filter. Remember the convolution for the MKS is
However, when the primitive basis is selected, the MKSLocalizationModel solves a modified form of this. There are always redundant coefficients since
Thus, the regression in Fourier space must be done with categorical variables, and the regression takes the following form:
where
This removes the redundancies from the regression, and we can reproduce the filter.